第７話　ごっちゃになっている強度の話

材料メーカで研究をしていた時のお客様と私の会話・・
[お客様]：強度の強いプラスチックの銘柄を選定してほしい・・
[私　　]：破断点強度の高い銘柄ですね。
[お客様]：そうそう！　大きな力をかけても変形し難いやつね・・
[私　　]：・・・・？

皆さん・・この会話で何がおかしいか、気づきましたか・・？
荷重が加わった時の材料の機械物性を全て【強度】で表現している人が結構多い様です。
機械物性についてちょっとコメントしますね。

材料に作用する力は「応力」で表現します。
「応力」とは作用している力(荷重と言います)を材料の断面積で割った力です。
例えば、10Nの力で丸棒を引っ張った時、1mm²の断面積の丸棒と10mm²の丸棒では、その材料にかかる負荷は全く違いますからね。
10mm²の丸棒の材料にかかる負荷は1mm²に比べて1/10になります。

もう一つ重要なのは材料の変形度合いです。荷重が作用した時の変形度合いを「ひずみ」と表現します。
「ひずみ」とは、荷重により伸びた(又は縮んだ)量を元の材料の長さで割ったものです。
例えば、100mmの丸棒をある荷重で引っ張って、丸棒が0.5mm伸びた時、「ひずみ」は0.005(又は0.5%)です。

では、一般的なプラスチックや鋼の場合は荷重をかけた時、「応力」と「ひずみ」の関係はどうなるのでしょうか。

下図は応力とひずみの関係を示したグラフですが・・

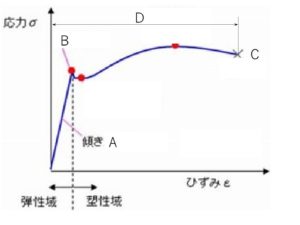
まず、荷重をかけて行くと、材料には応力が発生し、それに伴って、ひずみが生じます。

この発生する応力とひずみの関係は、図の青線になります。

ゼロの状態から荷重を増やして行くと、ほぼ比例してひずみが増え、B点に到達します。
ゼロからB点までは、双方はほぼ比例関係で、荷重を減じると、又、ほぼ青線に沿って戻ってきます。(プラスチックの場合は厳密には完全比例ではありませんが・・)

このゼロからB点までは、バネの様に荷重をかければ伸びるし、荷重を取り除けば元の形に戻りますので、この間を弾性域と言います。

B点以降は荷重をそれほど増やさなくても、ひずみは増えて行き、最後にはC点で破断します。

このB点とC点の間は荷重を取り除いてもひずみは元には戻らず、まるで、粘土の様に荷重をかけた時のままの形状になっていますので、この間を塑性域と言います。

荷重を取り除いた後、形状が元に戻らない状態は通常の製品では考えられませんので、普通はB点以上の応力が作用しない様に設計します。
例えば、椅子に座った時、体重で変形して座面が低くなり、その後立ち上がっても、そのままの状態になってしまっては使いものにならないですからね。

ここで、それぞれの名称を紹介します。

◇上図の応力とひずみの関係のグラフ：応力歪線図（SSカーブ）と言います。
(SSはStressとStrain)
◇傾きA：縦弾性係数、縦弾性率、又はヤング率と言います。[＝応力／ひずみ] この値が大きいと変形し難いです。
◇B点　：降伏点と言います。又、B点の応力を降伏点応力、降伏応力と言います。
◇C点　：破断点又は破壊点と言います。又、C点の応力を破断応力、破壊応力、
或いは引張強度、引張強さとも言います。
◇D　　：破壊ひずみ、破壊伸び、破断ひずみ、破断伸びと言います。

製品の部位によって、必要とされる機械物性はかなり異なりますので、材料メーカに銘柄選定を依頼する時は、具体的にどのポイントの物性が重要でかつ必要とされているかを明確に伝えた方が、より適切な銘柄を選定してくれると思います。